内涵与规则
这篇文章可能暗示(也是我在思考和写作时一直暗中在想的),分类谓词和投射谓词分别是如何在哈特式的描述法理学和德沃金式的解释法理学中找到自己的解释性力量的。
这是自《不要问意义,而要看使用》以来的系列文章的“终章”。在这篇文章中,我分别讨论了个体或具体对象的等同、抽象对象及属性的同等、规范和规则的逻辑等三个密切相关的基本问题,最终表明一切事情被归于在当出现一个对象 △ 则以一个殊型 ◇ 对应这一最简单的原子事实,要是我不愿意承认原子事实,那么除了原子对象之外,我就好像还得承认像规则、功能这样的奇特实体,不过我处理它的方式就是详细重述以下过程:每当出现一个对象 △,实际以一个殊型 ◇ 对应。我只会陈述它们,以关于实事的术语来陈述它。这篇文章可能暗示(也是我在思考和写作时一直暗中在想的),分类谓词和投射谓词分别是如何在哈特式的描述法理学和德沃金式的解释法理学中找到自己的解释性力量的。有关分配单称词项(DST)、规则矩阵、纯粹规则约束分类词和纯粹描述分类词的论述又暗示我是如何坚定地站在德沃金这一边的。问题永远比解决更多,而且更好的解决一向带来更好的问题。今天的结果,在我写[《无限与本质》](/2019-09-12-essence-and-infinity/时就有所预示。我一直在顺着隐约的方向摸索着。无论如何,这会是一个不错的结果和开始。
怎么理解(1)“a is b”呢?回答涉及“is”的逻辑结构,也因“a”和“b”的词项类型不同而不同。不过,请先考虑如果“a”和“b”都是名词,能否将它理解为
(1-a)a=b
呢?如果是这样,那么就是将“is”理解为等词。因此,(1-a)将(1)理解为是等同陈述。不过,当如果我们说(2)“Socrates is the teacher of Plato”时,我们不只是想说
(2-a)Socrates = the teacher of Plato
因为历史上的 Socrates 和 Plato 如果叫别的名字,我们也会有类似的表述。所以,我们期待(1)之类的表达更深层的逻辑,比如,有一个对象,它同时有两个名称,分别是“a”和“b”,于是
(1-b)(∃c)(a=c ≡ b=c)
这表示,存在一个 c,a 等于 c,当且仅当 b 等于 c。那么“c”会是我们要找的那个对象吗?在许多场合,(1-b)足够用的了。可是考虑下(2),这个更有信息的表示更容易让我们看出问题来,对它的期待会是表达如下逻辑结构吗?
(2-b)(∃f)(Socrates=f ≡ the teacher of Plato=f)
这表示,存在一个人,Socrates 等于这个人,当且仅当,the teacher of Plato 等于这个人。
这里有些含混,我想我们被名称和对象之间的混淆给弄糊涂了。当我们说“Socrates is the teacher of Plato”时,我们心中想到的是 Socrates 这个对象有“the teacher of Plato”的属性,我们没有谈论两个名称,而只是将一个属性归属于一个对象。当我们谈论(1)时,我们也会有这样的意思。这就把“is”理解为关系谓词。
总之,当我们说(1)之类的句子时,我们要么是说有个对象,它至少同时有两个名称,要么是说有个对象,它有某个属性(至少是说,它被某个谓词称谓)。
不过,想一想,我们还有其他一些想法,比如对于(1),我们想说的是,有个对象,无论它有什么名称,这些名称的意指都会是等同的。在这里,区分了两类东西,一类是对象本身,一类是名称。这就是说,总有个什么,它是所有名称命名的东西而本身不是名称。如果是这样理解(1),也就有
(1-c)(∃ INCONi)[(INCONj)(INCONj= INCONi .≡. INCONj is b)and INCONj = a]
这会是一个非常深层的逻辑结构[1]:存在一个不用名称命名的个体常项 INCONi(我们可以理解为对象的真身),对于所有的不用名称命名的个体常项 INCONj,它们都等于 INCONi,使得,INCONj 是b,并且正好 INCONj 等同于 a。要注意这里加粗的“是”表达了形而上学的事实,表明“b”就是那个对象真身原始的(primary)名称,而“a”是原始名称之外的偶然名称,换言之,“a”可以替代为“c”、“d”、“e”等等无论什么。在以后,当我在形式化的语言中使用“=”时,我总是用这个符号表示前后两个表达式是可相互替换的,或者说彼此是替身。
这表明,对于像(1)这样的句子,我们或许可以换作以下形式以更好的理解,因为上面的分析显然涉及到了关于“真”的问题:
(1-d)a is true of b
如果不要繁复的逻辑结果的说明,那么可以说(1-d)就很好地做了(1-c)所做的事情,即 b 是某个对象真身的原始名称,而“a”则是除“b”之外的任何一个偶然的名称。或者你可以将 “a”理解为是对象 b 的原始名称,此时你就将 b 理解为对象本身。这里对于 “true of”的逻辑重构表明,相关的名称必有一个在原始意义上的使用(这一点,参见塞拉斯《自然主义和存在论》第四章)
有人可能会说,这除了告诉我们有个不被命名的对象真身之外,等于什么也没说,这里有什么可大惊小怪的问题呢?
还记得我们过去一再提到的殊型和殊相的关系问题。我们说过,在原始意义上谈论的殊型和殊相关系是这样的:所有实际捕捉到的都其实是殊型,但必有某些殊型在原始意义上被假定是殊相,一旦说某个殊型是某个殊相,就是将它们等同起来,无法分清彼此。现在通过(1-c),我们更清楚地揭示了这内部是怎么回事。我想通过这个说的是,除了上面的话之外,还有关键的一点,就是殊相是不存在的,所有关于殊相(或者说对象)的谈论都是语言殊型的问题[2]。所谓对象的真身,一个不被名称和述谓的对象,只是一个逻辑构想,并不可能被实际设想。即便每个人都是精灵的化身,它比必须得有任何形式的显现才能被设想,而只要它显现了,就可用一个殊型对应。不过,这样,精灵背后的精灵仍然是在迷雾之中。
我们还没有考虑对(2)做归属给一个对象某属性的理解的情况。当然,要是(1)之中的“b”等于“the teacher of Plato”,下面对(2)的分析也适用于(1)。按照从(1-c)那里获得的启示,我们先把把(2)处理为
(2-c)(∃ INCONi)[(INCONj)(INCONj= INCONi .≡. INCONj is the teacher of Plato)and INCONj = Socates and the teacher of Plato is a predicate.]
这表示,对于一个非以名称命名的对象 INCONi,对于所有的非以对象命名的对象 INCONj,它们都等同于 INCONi,使得,INCONj是the teacher of Plato,并且 INCONj 有一个名称等同于“Socrates”,并且“the teacher of Plato”是一个谓词。我们似乎锚定了对象真身,指出那个对象被称谓了一个谓词“the teacher of Plato”。显然,这还未触及我们期待的属性(attribute)。因为,如果我们只是说,一个凑巧有“Socrates”名称的人有“the teacher of Plato”的称谓,则对于这个对象到底有什么属性,我们什么也没说。
看起来我们得作出一些改变。希望在于看到,“is”左侧这一方的“Socrates”所命名的对象,即同样具有右侧一方例示“the teacher of Plato”的对象具有的属性。所以我们放弃对“is”做等词情况的处理,转而将“Socrates”和“the teacher of Plato”等看作是具有属性的东西,或者是被某些个对象例示的抽象对象,即使只有一个对象例示了它们,而它(们)所以例示这个抽象对象,则是因为具有相同的属性。于是我们想说,可能是,无论什么对象,如果它例示“Socrates”的属性,就一定例示“the teacher of Plato”的属性,这样我们可以说,Socrates 实质等价于(material equivalent,ME)the teacher of Plato,即
(3)Socrates ME the teacher of Plato
不过,这不是我们想要的逻辑形式。我们需要将“Socrates”和“ the teacher of Plato”重构为分配单称词项(distributive singular term,DST),它是一个内涵语境的外延元语言,于是就有了我们想要的逻辑形式
(4)•Socrates• ME •the teacher of Plato•
加了点引号的表达式事实上成为殊型的普型。可以很容易理解这一逻辑处理。每个殊型都命名一个对象(殊相),同时例示(exemplify)[3]一个普型,一个普型指示一个抽象对象。这里关键是理解 DST 的内涵语境的外延元语言身份。一个 DST 执行分配一个单称词的功能,这个单称词完全是外延的。这里所发生的事情是,对于诸对象 a1、a2…an,依照在特定语境的需要,分配一个单称词给这些对象,用以概括表示它们。像•lion•这个 DST,表示全世界所有的 lion 个体。如果说“the •lion• is dead”,这意味着“•lion•s are dead”。所以你会看到,DST 随时可以变成复数词。要记住,殊型和普型都以书写(inscription)样式来表示,一个书写样式单独是没有任何语言内意义的。另外,至关重要的一点是认识到,一个 DST 表面上有的内涵语境,实际上不过是用元语言表示的外延语境。
这样,我们就有
(4-a)(x)x is a •Socrates• ≡ x is a •the teacher of Plato•
这表示,对于所有的对象 x,x 是一个•Socrates•,当且仅当,x 是一个•the teacher of Plato•。“is a”要被理解为“属于”或“包含于”而不是“等于某个”,这种用法的典型语境是“Man is an animal”。“is a”后面的词项要被理解为一个分类谓词(sortal predicate),后者执行特定的功能[4]。
现在我们有两条路径理解含有属性等同陈述的句子。第一种是内涵路径,它将这一情况理解为,之所以任何例示•Socrates•的殊型都必定是例示•the teacher of Plato•的殊型,正在于•Socrates•是•the teacher of Plato•。第二种是外延路径,它把这一情况理解为,之所以说•Socrates•是•the teacher of Plato•,正在于任何例示•Socrates•的殊型都实际例示•the teacher of Plato•。
怎么理解这两种路径呢。先看内涵路径。坚持这个路径的人将•Socrates•视为一个内涵语境(但不再是个 DST),并将•the teacher of Plato•视为一个外延语境(可以是一个 DST)。这会是如下情况,当确定例示•the teacher of Plato•的殊型之后,普型•the teacher of Plato•也就确定了,那么对于这个普型指示的抽象对象具有的属性也就确定了。重要的是,“Socrates”不仅仅是命名了这个抽象对象而已;如果仅仅是命名了这个抽象对象,那么以其他任何名字命名这个抽象对象将没有任何区别;这样,“Socrates”将表达一种内涵语境,意味着它是指示那个不以任何谓词称谓的抽象对象真身,并且对任何称谓这个抽象对象的谓词起到约束(bound)作用;正因这个抽象对象的约束作用,才保证了任何其他称谓它的谓词被特定的殊型例示。用普通人的话说就是,苏格拉底就是苏格拉底,只有苏格拉底才是柏拉图的老师。这一路径在日常的语境中有非常频繁的使用。我们说,(以一个特定的谓词称谓)“Alcibiades is treacherous”,我们会说,“treacherous”这个谓词尽管可以是外延的,可以通过考察发现是哪些确定个体被这个谓词所称谓。用别的什么叫法,比如“不义”来称谓这些确定的个体也无所谓,但重要的是,这些偶然的称谓最终指向一个无需称谓的抽象对象,正是它使得那些谓词称谓了那些个体。我们可以从以下逻辑结构中感受这一点:
(4-a-I)(∃ PRECONi)[(PRECONj )(PRECONi = PRECONj .≡. PRECONj is the teacher of Plato)and PRECONj = Socates].
其中的“PRECONi”是无需谓词称谓的常项(predicate constant),表示那个抽象对象的真身。这表示,存在一个指示抽象对象真身的无需谓词称谓的常项 PRECONi,对于所有的 PRECONj,都等同于 PRECONi,使得,PRECONj是the teacher of Plato,且 PRECONj 等同于 Socrates。
显然,“the teacher of Plato”扮演了那个抽象真身的原始谓词的角色,尽管它是 PRECONj 的一员(一个偶然的可能项)。由于 PRECONi 和 PRECONj 都是没有谓词称谓的,所以实际上所能获得的只有“Socrates”之类,但“Socrates”只是除了原始谓词之外的其他任何一个偶然的谓词。前者仅仅是对后者任何在原始意义上使用的一员的逻辑构想。
当然,不妨对照(1-c)来理解这里的“Socrates”和“the teacher of Plato”分别扮演的角色。同(1-c)所带来的困惑类似,这里除了只是说有个抽象对象真身使得任何其他指示它的谓词称谓了特定的个体之外,我们还得到了什么?拿掉任何已经确定了所实际称谓的个体的谓词,这个 PRECONi 到底是什么?它是个黑洞,里面要么什么也没有,不允许说它称谓的任何个体,因为它是不被任何谓词指示的,而且一旦要详细说明它被哪个谓词所指示并且该谓词称谓了哪些特定的个体,就必须以外延的方式详细说明,这样它就不是 PRECONi 了[5]。
所以,对内涵路径的关键诘难是,除了提供一个空洞的名称作为一个有确定外延的 DST 的别名,还说了任何别的有用的信息吗?这个空洞的名称,可以被完全理解为任何一个对象,而任何一个对象都可以由任何无论什么名称的命名。内涵路径带来的后果是,换来一个顶多与具体对象无异的空洞的抽象对象。我想不到坚持内涵路径的人如何对这类诘难自圆其说。
现在让我们考察外延路径。坚持这个路径的人认为,•Socrates•和•the teacher of Plato•都是 DST,都执行分配一个单称词的功能,这个单称词是用来对任何一组确定对象的概括表示,它不是一个名称,也就是说没有任何指称,只是那一组确定对象的缩略表示:它们可以共同拥有一个名称,但并非由于任何属性。或者如果你愿意,把它看做便捷称呼就好了[6]。这样,(4-a)的意义就更明白了。以这种路径来理解两个抽象对象以及属性的同一性,对(4)和(4-a)的处理就会是像
(4-a-II) •Socrates• ≡ •the teacher of Plato•
这样的形式,这大概表示一个比实质等价更强但仍然是外延的逻辑,说的是,任何对于一组对象而言,若它们例示•Socrates•则就一定例示•the teacher of Plato•。表面上看,这会具有
(4-a’)Ki ≡ Kj
的形式,并且再次回到了(4a)。
可见内涵路径和外沿路径会在表面上汇聚在(4a)上,但对它的解释不同。首要的一点是,对于像(4-a’)这样的形式,如果执行外延策略,要求 ≡ 前后的普型都是 DST,这意味着它们所分配的单称词则完全彻底殊型化,则所有的例示对象都得到命名并被确定。正是在这里,内涵路径和外延路径发生激烈的争夺:内涵路径主张,“≡”前后的普型都是某个抽象对象的偶然的名称,而正是由于这个抽象对象才使得命名它的任何普型的例示对象相同,进而说任何这样的普型等同;外延路径则坚持,说两个普型等同,无非是说例示它们的对象正好相同,这背后并非所谓抽象对象保证了这些对象正好相同。显然,在外沿路径中根本找不到属性的位置,因为拿掉属性,这个可以可被柏拉图主义者视为抽象对象在例示它们的具体对象的中的分有的东西一旦被拿掉,抽象对象本身就会崩溃。
到这里问题已经很清楚了。如果我们对此还有疑问,就可以更一般化地看待像
(5)•f•≡•g•
这样表面上看似表示普型等同的形式,其中如果只有•g•充当 DST,即它是彻底外延的,而如果像内涵路径那样以•f•充当一个接近 PRECON 的角色,又会发生什么呢?马上发生的事情就是,除了提供一个空洞的抽象对象名称之外,对•g•的例示对象什么也没说!这个 PRECON 不叫•f•又何妨?它叫别的任何东西又何妨?这个 PRECON 是别的任何 PRECON’又如何?它既不被称谓,又不被例示,它什么都不是,或者什么都是。
仔细考虑•f•和•g•均未殊型化的情况,面对没有任何殊型的普型,似乎我们就得承诺
•独角兽•≡•龙•
进而
独角兽=龙
由此类推,只要•f•和•g•都未殊型化,那么它们可以是任何东西。我们曾说过,sense(意义)是语境中常常出现的最稀薄也是最根本的关于有所言说的术语,我们能否说
(6)si is the same as sj .≡. si≡sj(si 相同于 sj,使得, si,当且仅当,sj)?
要是 si 和 sj 都没殊型化,我们不得说,任何 si 都相同于 sj 吗?这意味着任何没有说出来或说清楚的意思都将是相同的。这无疑是对内涵路径的尖刻的嘲讽。
在塞拉斯与迈克尔·洛克的通信中,洛克斯曾这样抗议:
为何•Socrates•与•the teacher of Plato•有共同的外延……正是因为 Socrates是the teacher of Plato……一直靠(不管怎么加固的)实质等价这个元语言权宜手段来谈论定义等同是执迷不悟,本末倒置了。(塞拉斯《自然主义和存在论》,“与迈克尔·洛克斯的通信”,第 15 段。)
塞拉斯说,正是在这里,洛克斯摊牌了。在我看来,他摊开了自己采取内涵路径的底牌。至于孰是孰非,就留给读者自己评判了。
我在这一点上追随塞拉斯,但对洛克斯的抗议中所暗示的形而上学上的直觉耿耿于怀。洛克斯的抗议无疑有形而上学方面的诉求,它要求我们承认在有关“Socrates is the teacher of Plato”之类的陈述中蕴涵了某些形而上学事实。我们能轻易打发这个提示吗?难道真的不是由于确实有那么个人,他具有是柏拉图的老师的属性,才使得“Socrates is the teacher of Plato”为真的吗?这个关于形而上学的争论会把我们带到关于真的争论中,而我们已经在前面的文章中说明了后者的本性。
不过,既然对此耿耿于怀,那应该有中和之道。这就是,如果我们既想表达这样一个观点,即任何落入•f•的对象都必定落入•g•之中,我们不是在作陈述,而是在表达规范。如果是在作陈述,则当且仅当•f•和•g•都充当一个 DST,并且有完全相同的外延时,我们才说它们是等同的。这肯定是已经实际发生的事情。如果我们不满足于已经实际发生的事情,并期待将来每当一个对象落入•f•中,就必定也会落入到•g•中,反之亦然,那么我们就在表达规范。规范是由某个规则保证的,任何在该规则前件集合中的对象,也必定实际在规则的后件结合中有对应的对象。这不是在表达什么必然性,而是规范性,这会有一个像
(7)f-ness≡g-ness
形式的表述。它构成对(5)的约束,面向过去和未来,使一切当前还不明确的以后都可以明确起来。这就要求,对于普型•f•来说,每当归入一个对象(或说每当捕捉一个对象),则都向普型•g•归入这个对象。一个类似的要求是,每当在•f•的殊型构成的集合中确定一个对象,都在•g•的殊型构成的一个集合中确定一个对应的对象,以确保两个集合一一映射的关系。还可以有一个类似的要求,即每当确定或捕捉到一个对象,则向其同时投射普型•f•和•g•所表示的谓词(进而这些谓词会对这个对象执行它们在特定的语境中的功能)。最后一个要求最类似于实践。
我想可以说,规范或评价的活动是一个内含事实或陈述的活动。用我们的术语说,“f-ness≡g-ness”之类的事情内含一个关于“•f•≡•g•”的事情。现在请想一想这个陈述(这以下许多都是塞拉斯的例子):
(8)Trespassers are prosecutable
它具有如下表面上的逻辑力量:
(x)x∈T ⊃ x is prosecutable
但这是个错误。想一想,如果把 trespassers 和 prosecutable 殊型化,则有
•trespassers•≡•prosecutable•
这里•trespassers•和•prosecutable•都充当 DST,且完全是外延的,会有如下的逻辑形式
(x)x is a trespassers ≡ x is prosecutable
你会发现这个双条件句的右手边有些奇怪,因为它不是“x is a prosecutable”,如此才能完全与左手边对应起来。“prosecutable”谓词的类型阻止了我们这么做;究其原因,它是个投射谓词(这个词我从古德曼那里获得的启示),而不是分类谓词。一个投射谓词面向过去、现在并特别是面向未来,而一个分类谓词就是充当 DST 的谓词,它仅面向当前特定时间和地点(语境)的能够确定的全部对象,换句话说,分类谓词只对现在负责。
我们说过,一个规范内含一个事实(这似乎是大白话),现在让我们充分地解释这一点。(8)初步的逻辑形式可以是像
(8-a)Permitted[(x) x∈trespasser ⊃ x is prosecuted ]
它表示,允许以下(齐一性)事实发生[7],对于所有的个体 x,x 属于擅闯者,那么 x是被起诉的。如果我们通过(8)想确切表达的意思是
(9)Let all trespassers be prosecuted
那么它具有形式
(9-a)Let[(x) x is a T ⊃ x be prosecuted]
如果我们明确是在表达一个规范要求,则它会是
(10)All trespassers are ought to be prosecuted
具有如下形式
(10-a)‘Let[(x) x is a T ⊃ x be prosecuted]’is valid
无论如何,(8)~(10)不同于
(11)All trespassers are prosecuted
它具有形式
(11-a)•trespassers•≡•prosecutable•
也就是(10)。我们说过,在像•f•≡•g•之类的逻辑形式中,“≡”两侧的普型都充当 DST。(8)~(10)不会衍推(11),也不被(11)所衍推,这就是事实与规范之间的鸿沟。不过,我们会看到这个表面上的鸿沟是怎么弥合的。
无论如何,当我们将“f-ness≡g-ness”看成是相对于“•f•≡•g•”表示的事实的规范表示,我们就区分了以下两种情况:
(1)对于“•f•≡•g•”,其中当任何一个对象被投射以普型•f•表示的谓词,则实际投射给了普型•g•表示的谓词。这可以看作记载一个规范事情的历史事实。正如对任何一个人,如果他曾是杀人犯,都实际被处以死刑。
(2)对于“f-ness≡g-ness”,其中当任何一个对象被投射以普型•f•表示的谓词,则应当投射给普型•g•表示的谓词。这可以看作是说明一个规范事情正在进行的事实。
在特定时刻所获得只会是有“•f•≡•g•”形式记载的一个历史,这个历史仅仅表明•f•和•g•所表示的谓词以及该谓词被假定所指示的抽象对象都仅仅是个对表面上的内涵语境的外延元语言对象,一个 DST,即一个分类谓词,它只对特定时间和地点的所有确定对象负责。
在一个分类谓词中寻找抽象对象是徒劳的;如果一个规范的事情正在进行,则寻找相关的抽象对象的正确方式不是寻找已经造成的无数分类谓词,而是将其看做是不断展开的叙事,其中不断产生分类谓词,直到这个规范的事情终结;只是在一个规范的事情终结之时,才能勉强谈论一个抽象对象,因为那个最后生成的分类谓词最有资格指示 PRECON。与内涵路径将 PRECON 视为支配历史过程的在先存在的做法恰恰相反,外沿路径将 PRECON 看作是历史终结之时的最后产物。我们不妨把一个规范的事情叫做实践。
还有许多细节值得我们深究。现在想一想(10-a),假如起诉擅闯者的事情从未实际出现,而且可能永远也不会出现,这就如同设想一个永远不会被实际玩的游戏,那么我们是不是得遭受一个当初提给内涵路径的相同异议呢?的确可能是这样,因为这意味着“f-ness≡g-ness”内包含的事实“•f•≡•g•”是空的,因为•f•和•g•都没有任何殊型。那么我们不得说,任何没有实际发生的•f•和•g•都相同吗?如果一个实践正在发生,除了已经产生的分类谓词之外,外延路径提供的投射谓词所讲述的故事不一样空洞吗?这个异议现在坚持:如果说没有殊型化的任何普型都可以是相同的,以至于提一个在先的抽象对象是空洞的;那么对于一个投射谓词尚未殊型化的(未来)部分,不一样是空洞的吗?事情不还得是这样,即我们毕竟得满足于一个有关分类谓词的事实陈述吗?
对这个异议的答复正在于提醒内涵路径的坚持者,所谓任何有关分配谓词所陈述的事实,都是投射谓词制造的结果。一切事实,如果它被理智所设想、感知和思想,都是规则生成的。没有独立于规则生成过程之外的独立事实作为规则生成的标准。这可以从有关是与应当的本性和关系,有关真与谓述的本性和关系中看出;就另外一个问题而言,这是理由和原因的本性及其关系的问题,在这里就不多赘述了,前面的系列文章已经有所论述,相信足够我们明白相关的想法了。
为了使这一点更清楚,让我们看看投射谓词是如何工作的。请先考虑“•f•≡•g•”,它类似于“Ki≡Kj”,我们根据一条类似于莱布尼茨的原则(L)有
(L)The Ki is the same as Kj ≡ every context which is true of the Ki is true of Kj
这会遇到空类的问题,由此任何任何适用于独角兽的语境都适用于龙。不过,古德曼会说,虽然独角兽和龙都没有殊型,但至少它们有不同的殊型•独角兽•和•龙•,两个空洞的名称。塞拉斯认为这不过是权宜之计,假设它们甚至没有任何普型,而以占位来表示,对于都没有任何殊型的 Ki 和 Kj 来说,有如下图式
Ki is the same as Kj .≡. Ki≡Kj and ☨Ki☨≡☨Kj☨
其中加 ☨ 引号的 Ki 和 Kj 是任何加•引号的殊型带入后的结果,这也不会解决问题,因为“☨Ki☨≡☨Kj☨”部分最终会是空的,因而会回到“Ki is the same as Kj .≡. Ki≡Kj”,最终任何没有殊型化或没有殊型的普型适用于任何一个语境,这会是非常空洞的。
现在,塞拉斯引入“hold of”作为“true of”的替代,二者之间的关系是普型和殊型的关系,即前者有概括指示的功能,表示一组殊型与相应的对象对应,后者则用于其中一个特定的殊型与相应的对象对应。那么就有了一个得到修改了的原则
(L’) (L)The Ki is the same as Kj ≡ every context which holds of the Ki is true of Kj
“hold of”字面上有抓住或把握住人或物或者完全控制、影响某人或某物的意思。我理解,塞拉斯将其引入到这里作为“true of”的替代,正是利用了它兼具针对特定个体发生作用的具体情况和对诸个体起全面作用的概括情况的意涵。
有了这些准备,让我们继续考虑
(10-a)‘Let[(x) x is a T ⊃ x be prosecuted]’ is valid
我们以这样一个方式来引入表述“hold of”,即
(12)‘Let[(x) x is a ⊃ x be prosecuted]’ holds of trespassers
它逻辑等价于(10-a),一般化的形式是
(13)‘Let[(x) x is a K ⊃ x be φ’d]’ is valid
这个一般形式逻辑等价于
(14)‘Let[(x) x is a ⊃ x be φ’d]’ holds of Ks
现在可以考虑下塞拉斯所举的一个例子,一个从未玩过的游戏,其中的“pawn”(兵)和“bishop”(象)分别是如下对象,即已经做出或将做出 pawn 走式的对象和已经做出或将做出 bishop 走式的对象。用“Mp”表示可接受的走兵的合取,每一个合取肢具体说明某些移动在什么条件下被许可。设“Mb”表示相应的走象的合取。依照(L),会有
The pawn is the same as the bishop
因为这个游戏实际不会被玩,所以既没有任何走兵的对象也没有任何走象的对象。但(L’)告诉我们兵不同于象,因为
‘Let [(x)x is a ⊃ x be Mp’d]’ holds of pawns but not of bishops
而
‘Let [(x)x is a ⊃ x be Mb’d]’ holds of bishops but not of pawns
这样,即使实际没有诸兵和诸象,兵也会不同于象。根源在哪里呢?在于这里的规则。一个规则一样的表达式是一个具有形式
‘Let[(x) x is a ⊃ x be φ’d]’
的一般祈使句。塞拉斯引入了规则矩阵(rule matrix)的术语,即
‘Let[(x) x is a ⊃ x be Mi’d]’
然后说它是一个对于例如诸 Ki 有全面支配并会(shall)实际捕捉到特定的它(们)的规则矩阵,于是可以说
The Ki is normatively the same as the Kj
当且仅当
Every rule-matrix which holds of Ki holds of Kj and vice versa.
然后引入纯粹规则约束分类词(pure rule bound sortal)、纯粹描述分类词(pure summary sortal)和混合规则约束和描述的分类词(mix sortal) :
(I)一个纯粹约束分类词其意指公设仅用规则矩阵
x is a Kpr =‘Let[(x) x is a ⊃ x be Mi’d]’ holds of Kprs
来详细说明。
(II)一个纯粹描述分类词其意指公设仅用描述标准
x is a Mi’d ≡ x is Φ1, …Φn
来详细说明,注意它是完全外延的!
(III)一个混合规则约束和描述的分类词其意指公设即涉及描述语境又涉及规则矩阵。
最后让我做一些简短的评论来结束这篇略显冗长的文章。让我们再仔细考虑下
(13)‘Let[(x) x is a K ⊃ x be φ’d]’ is valid
(14)‘Let[(x) x is a ⊃ x be φ’d]’ holds of Ks
它们逻辑等价。(14)中“”如何理解呢?它实际是一个占位。我在前面的文章多次提到它。它表示,每一次执行规则,将实际捕捉到一个对象,这个对象将被补充到一个占位中,一旦占位被实际补充,那么一个对象就如其所是,但是在此之前,就什么也没有,也许除了规则。
现在想想休谟的闪电-雷声序列和闪电印象-雷声印象序列。对此我暂时没有发现有我在《规则和对象》中对休谟式的实践推理的评论更贴近地表达我现在的想法的了,我把它摘抄如下:
可以说,休谟的世界中缺乏一般哲学家所说的实践和实践推理的事情。仔细回想《人性论》中的“道德学”和《道德原则探究》,可以发现,由被动的印象推论反推自然推论的冲动一直都在,但并未最终爆发出来。简单地说,休谟式的实践推理的基本形式是这样的:(1)如果过去总有 b 印象伴随于 a 印象之后,那么现在当 a 印象出现,随后伴随 b 印象,人们就会感到愉悦。实际情况中,当 a 印象出现时(此时殊相 a 是现实的),可能唤起 b 观念(此时殊相 b 只是被期待的),正是这个观念有使人行动的冲动。(2)如果一种可确定的可重复项在过去一直出现,则人们就有从这一外延事实获得对某种内涵属性的期待:类似的重复项将继续出现,好像它们例示内涵属性的具体实例。正是在这个地方,“是”向“应当是”奋力跳跃。每当这一期待不被落空时,人们都感到愉悦。休谟对以下情况没有多大信心:(1)为了得到 b 印象,制造 a 印象;(2)为了得到某种内涵属性,继续制造可重复项。
休谟在实践哲学上的困境在于他的核心术语印象的本性摇摆于意象和思想动作两种意义上,正是由于这一摇摆,他的世界中只有“是”(bes)与“应当是”(ought-to-bes)而缺乏“应当做”(ought-to-dos)的位置。这使得他的道德哲学缺乏坚定和清晰的行动观念。
现在,塞拉斯对休谟的推论理论的批评就在于,它缺乏关于“应当做”的实践推论。我们看到,休谟只对于得到自然推论补充和强化的印象推论有信心,因为这里展现了最确定的齐一性(uniformity):
闪电 闪电印象 雷声 雷声印象 ……
回顾起来,会发现一直以来有两组靠相像而关联的序列并行出现。把这里发生的事情转换成言语行为的话,就会是这样的:
(I)每当环境中出现殊相 △,发出殊型 ○。此时,我们获得了情境-陈述的齐一性。
(II)△-○ 的配置进入到语言网络之内,必须遵循这种语言的句法规则和经验规则。对于句法规则,涉及到陈述的配置方式(英语和汉语为了表达相同的情景,其具体的配置显然不同)。对于经验规则,就如同在环境中区分两块石头一样,你不能在英语的某段上下文中说命题“a is red”和命题“a is green”同时成立,这不只因“red”的书写样式本就不同于“green”,更因为“red”和“green”在英语中发挥的功能并不同一。由此,我们获得了陈述-陈述的齐一性。
(III)当先说“我将举起手”,并举起手时,我们就从陈述-陈述的齐一性转场到情境-陈述的齐一性,但这次的殊相 △ 是我们有意使之现实化的。由此,我们获得了陈述-情境齐一性,与情境-齐一性有不同的身份:前者是“应当做”,后者是“应当是”。正是这里,休谟犹豫不决,缺乏信心。
为什么休谟会犹豫不决是个很复杂的问题,因为请看
△
○
△
○
把第一组齐一性看作是手-“手”,说的是在一个环境中出现手,则发出“手”的声音。如果从这组齐一性跳跃到第二组齐一性,表面上还是手-“手”的齐一性,即这里的环境中又实际出现了手,并发出“手”的声音,但实际上,这里的手只是与第一组齐一性的环境中的手相似。记住,你只能说它们相似,更没法说它们同一,也不能断定它们是例示手-类的实例(这个问题相当棘手)。但毫无疑问的是,在两组齐一性的两个环境中,“手”无疑是最相似甚至同一的,作为名称,它们无疑例示了自己所属的语词的功能。
休谟的犹豫也是谨慎。在《人性论》论述抽象观念的一节,休谟夸赞贝克莱对“当心灵想到这些观念时,这些观念是一般的,还是特殊的”问题的回答,称它为“近年来学术界中最伟大、最有价值的发现之一”,这个见解是:
一切一般观念都只是一些附在特定名词上(certain term)的特殊观念,这个名词给予那些特殊观念以一种比较广泛的意义(extensive signification),使它们在需要时唤起那些和它们相似的其他各个观念来。(休谟《人性论》,商务印书馆,第 26 页)
他的意见很明确,用我们的话说,只可以断定语言殊型的同一性而不能断定语言殊型所对应的殊相的同一性,也真是由此才有所谓例示抽象对象的具体对象与抽象对象的关系。同一的语言殊型的竹签串联了表面相似的殊相的烤羊肉块。
休谟谨慎的理由是,在手-“手”的例子中,误解重复出现的殊相-殊型序列中的项目各自的本性及它们的齐一性关系的问题还不算严重(至少是在相对稳定的日常认知状态中),但在更广泛的科学研究、重要社会实践和哲学论证中隐藏着巨大的危险。这个危险就是,认为每次出现的殊相 △ 都是例示某种内涵项目(属性或抽象对象)如 △-性的的实例,并进而将每个这样的实例与相应伴随的殊型 ○ 的齐一性认为是这样的事情:确实由于每当是一个 △,才以一个 ○ 对应于它;每个 ○ 的出现都依赖于每个是 △ 的项目的实际出现。这会形成一个规则,并且这规则每执行一次都是这样的事情:是 △ 的事实出现,于是以一个 ○ 对应于它。
我曾说过,事情可能恰恰相反,事情不是,每当是 △ 的事实出现,于是以一个 ○ 对应于它;而是,每当向过往的诸 △ 所在的序列的最后一个 △ 后的占位(place holder)上确立一个 △,就是向那个占位投射一个 △。不过,一旦投射实际完成,则不妨说事情是这样的:每当是 △ 的事实出现,才以一个 ○ 对应。正如每当一个出轨的男人出现,才以一个“渣男”的标签对应。但千万不要忘了这重复的 △ 序列中的各个项目的本性,它兼具“是”和“应当是”,因为正是由于将 ○ 实际投射到了什么上面,什么才现实化为完满的 △。正如实际给某个男人贴上了“渣男”的标签,才实际有渣男。
还有我在《推论和规范》中的一段话:
规范的事情就是这样的:一个规则的两端(前件和后件)组成的两个集合,当一个个体被归入前件后,则向后件的集合中的一个占位投射谓词,使之现实化和个体化;所以,一切规则后件集合中的个体都是被创造出来的,而所谓这些个体例示的属性或抽象对象只是这些个体的元语言对应,执行一个分配单称词项(DST)功能,这个元语言对应可能会随着个体的归入而不断扩张,因而表面上使得所谓属性或抽象对象持续变更内涵,以至于非到相关实践终结之时,其实并没有任何属性或抽象对象,而实践,正是更大范围的规范活动系统。
也许我的读者还有种种疑惑,更想对我提出种种纠正。我能够部分理解他为什么会疑惑,假使他已经仔细阅读了我最近的几篇文章。我想,关键的一点在于,正是对于殊型和殊相的关系问题上存在的混淆,使我们把规则、事实、是与应当等问题想的太过复杂但却收获甚微。
我坦诚,一个唯名论的外延主义者从最简单的假定开始看待这个世界(其中包括人类的活动):实际并没有殊相,只有与之接触的殊型,殊相仅仅被假定不会被捕捉;在不同的语言层次,在原始意义上使用的殊型就等于殊相;任何殊型对假定的殊相的接触都是规范的事情;任何事情无论多么复杂都根本上归于殊型及其对殊相的接触;任何殊型都仅仅是相似,没有任何同一的殊型,除非只谈“a”,只要谈论像“a=b”或“a is b”或“a is true of b”,就实际是在谈论两个殊型,并且在特定的语言层次,将其中某个殊型作为原始意义的殊型使用,即被视为殊相。
当问题来到任何两个集合、任何两个抽象对象、任何两个殊型,任何两个殊型对应序列以及任何特定语言层次的殊型-殊型对应序列,任何的谓词投射活动,都是类似于下面的图式的事情:
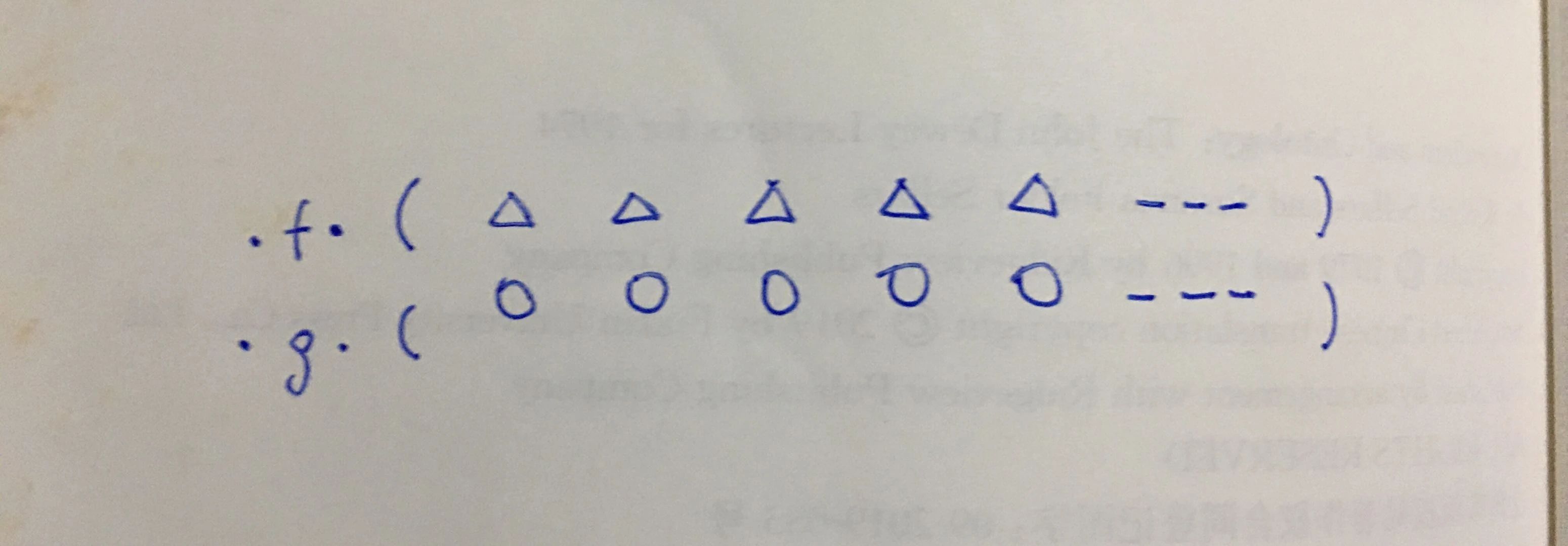
相信我的读者能够体会我手写这张图式而不是在键盘上敲出相应字符的用意。这个图式特别适用于作为一个初级唯名论的外延主义者对世界的基本理解。
2020/3/21 南坪
ᵀ、ᵗ、𝑡、𝒯、𝓣、𝓽、𝕥、𝕿、𝚝、𝙏(in L) is t